January 2017
The
TofJs project is published on the dedicated domain
TofJs.org.
The
caretaker-in-a-project-house package, the first product built on this architecture, has been moved to that domain, too.
November 26, 2016
Caretaker in a Project House
is a program with a browser GUI to manage and maintain digital project.
September 5, 2013
The Canvas Handbook is published, along with a
forum page for comments and remarks.
March 30, 2012
A new page for the
Change Logic project
is created and soon to be populated with new material.
March 25, 2010
A 5-pages paper called
Change Logic and the Change in Logic has been added.
February 2, 2010
The Haskell
PropLogic package is published along with related papers and other updates.
November 4, 2009
Descriptions of some major and minor projects have been added or improved (see
list of projects).
October 5, 2009
This homepage has undergone a complete makeover. A couple of new small texts have been added already, some bigger and big items are awaiting a final touch and should be added soon as well.
September 28, 2009
To increase the interactivity of the whole project, a
blog
was created, using the easy way provided by
blogger.com.
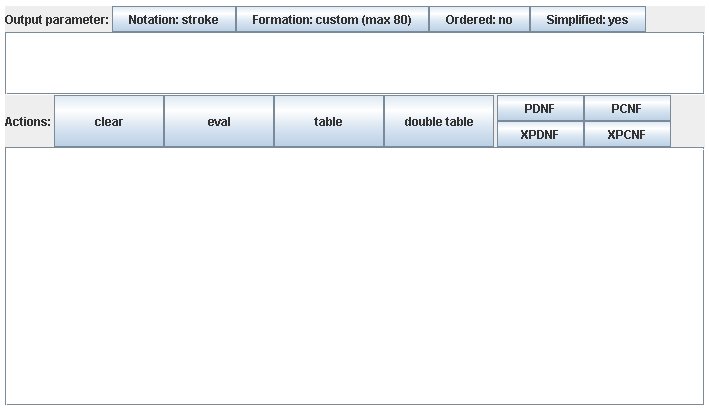 There is an online
Java applet,
a kind of pocket calculator for propositional logic.
It provides common features like the evaluation of a formula or the construction of its truth table.
But its real power is the generation of prime canonizations.
Next to the
applet
itself, there is also a separate
guide.
There is an online
Java applet,
a kind of pocket calculator for propositional logic.
It provides common features like the evaluation of a formula or the construction of its truth table.
But its real power is the generation of prime canonizations.
Next to the
applet
itself, there is also a separate
guide.


