
bucephalus.org
Algebraic properties of hyper-digital logic
online since July 2007
Abstract
Having defined the syntax and semantics of hyper-digital logic
(see [1]),
this paper investigates the basic properties of the quasi-order relation on hyper-propositional formulas of a given carrier set A and degree k.
One set of properties immediately derives from the fact that these formula algebras are quasi-boolean algebras. We for example have
- the idempotency of conjunctions:

- the associativity of disjunctions:

- the law of double negation:

Another set of properties involves the "box" and "diamond" operators and many results are similar to axioms and theorems of modal logic, such as
- the duality of box and diamond:
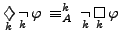
But not all phenomena fit into the perspective of traditional logical systems:
- If say
 is the carrier set then
is the carrier set then

-
Let S and T be two carrier sets, S a subset of T.
In traditional propositional logic, we can always increase the carrier set at any time in the sense that
 always implies
always implies
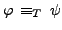 .
But this is no longer true in hyper-propositional logic, where for each degree k there are two formulas with
.
But this is no longer true in hyper-propositional logic, where for each degree k there are two formulas with
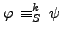 and
and
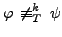 .
.
From a deeper point of understanding of course, these "surprising" phenomena turn into perfectly normal behaviour.
The text
The full text is currently under construction.
References
[1]
Hyper-digital logic: Summarized overview of its syntax and semantics
 bucephalus.org
bucephalus.org


